Number System (Binary, Decimal, Octal, Hexa-Decimal): Definition, Types, Conversion & Examples part-1
 |
| Types of Number System |
1. Binary Number System
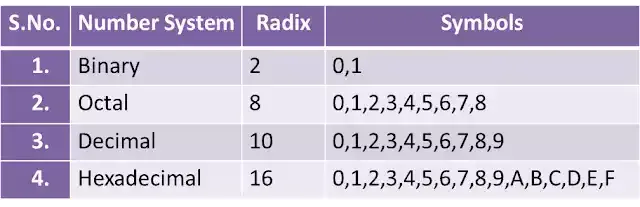
The binary Number System consists of two digits, namely 0 and 1. The base of the binary number system is 2.
For Example – (1011)2 is a binary number. The subscript 2 at the end of this number indicates the base of the number.
2. Decimal Number System
The base of the decimal number system is 10. In this, there are 10 digits as they are called 0,1,2,3,4,5,6,7,8,9.
For Example – (76)10 is a decimal number. The subscript 10 at the end of this number indicates the base of the number.
3. Octal Number System

The base of the octal numbering system is 8. In this, there are 8 digits as they are called 0,1,2,3,4,5,6,7.
For Example – (45.8)8 is an octal number. The subscript 8 at the end of this number indicates the base of the number.
4. Hexadecimal Number System
The base of the hexadecimal number is 16. Its digits range from 0-9 and A-F. For Example- (2BCF3)16 is the hexadecimal number system, and the subscript 16 at the end of this number indicates the base of the number.
The table below gives the hexadecimal numbers and their equivalents in decimal and binary forms.
Decimal | Hexadecimal | Binary |
0 | 0 | 0000 |
1 | 1 | 0001 |
2 | 2 | 0010 |
3 | 3 | 0011 |
4 | 4 | 0100 |
5 | 5 | 0101 |
6 | 6 | 0110 |
7 | 7 | 0111 |
8 | 8 | 1000 |
9 | 9 | 1001 |
10 | A | 1010 |
11 | B | 1011 |
12 | C | 1100 |
13 | D | 1101 |
14 | E | 1110 |
15 | F | 1111 |
Binary Conversions
i. Decimal to Binary Conversion:
In this method, the decimal number to be converted is repeatedly divided by 2 until the quotient becomes 0. The remainders 0’s and 1’s so obtained are then read in the reverse order to obtain the binary equivalent of the decimal number.
Example – (76)10 = ( )2 ?
 |
| Decimal to Binary Conversion |
[Remark: The remainder obtained in the initial division is the LSB (Least Significant Bit) & the remainder obtained in the final division is the MSB (Most Significant Bit).]
The equivalent binary number is (1001100)2.
If there is a mixed number, for instance 76.7, first convert 76 into its binary equivalent as above and then convert 0.7 into its binary equivalent as below.
Product | Fraction |
| Carry |
0.7*2=1.4 | 0.4 | and a carry of | 1 |
0.4*2=0.8 | 0.8 | and a carry of | 0 |
0.8*2=1.6 | 0.6 | and a carry of | 1 |
0.6*2=1.2 | 0.2 | and a carry of | 1 |
0.2*2=0.4 | 0.4 | and a carry of | 0 |
0.4*2=0.8 | 0.8 | and a carry of | 0 |
0.8*2=1.6 | 0.6 | and a carry of | 1 |
0.6*2=1.2 | 0.2 | and a carry of | 1 |
0.2*2=0.4 | 0.4 | and a carry of | 0 |
-------And so on-------- | |||
The equivalent binary number is (1001100.101100110)2.
If necessary, this process can be continued further when greater accuracy is desired.
ii.) Octal to Binary:
For each octal digit, write the corresponding binary digit. The same procedure is to be followed to convert fractional parts also.
Example – (45.312)8 = ( )2?
Octal Digit: 4 5 . 3 1 2
Binary Equivalent: 100 101 . 011 001 010
The binary equivalent number is (100101.011001010)2.
iii.) Hexadecimal to Binary:
Convert each hexadecimal number to its 4-bit binary number. Refer to the table to find the equivalent binary number. The same procedure for the fractional part was also followed.
Example- A3FE.2E16 = ( )2
Solution:
A 3 F E . 2 E
010 0011 1111 1110 . 0010 1110
The equivalent binary number is (1010001111111110.00101110)2.
Decimal Conversion
i. Binary to Decimal Conversion
The Decimal equivalent is obtained by multiplying each binary digit by its positional value. The rightmost bit has a positional value of 20. The second rightmost bit has a value of 21 and so on. And the leftmost bit has values 2-1 and so on.
Example – (10.011)2 = ( )10?
= 1*21+ 0*20+ 0*2-1 + 1*2-2+ 1*2-3
= 2+ 0+ 0+ 0.25+ 0.125
= (2.375)10.
Octal Conversions:
i.) Binary to Octal:
Begin by breaking the binary number into groups of three digits both toward the left and add the right of the binary point. If necessary, add binary digit 0’s at each end to complete a group of three digits. Replace each group of three digits with its octal equivalent (as shown in the table below).
Octal Number | Binary equivalent |
0 | 000 |
1 | 001 |
2 | 010 |
3 | 011 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
When Broken Up: 011 011 . 010
Octal Equivalent: 3 3 . 2
The octal equivalent number is (33.2)8.
iii.) Octal to Decimal:
Multiply each digit of the octal number by its positional value and add up the result.
First, convert an octal number to its equivalent binary number, which is then converted to its decimal equivalent. (As we have converted in the previous section).
Solution: = 2*82 + 3*81 + 7*80 +2*8-1
=128+24+7+0.25
= (159.25)10.
Octal: 2 3 7 . 2
Binary: 010 011 111 . 010
Decimal: 1*27+1*24+1*23+1*22+1*21+1*20+1*2-2
= 128+16+8+4+2+1+0.25
= (159.25)10.
iv). Decimal to Octal:
To convert the integer part of the decimal number, use the method of successive division by 8 until the quotient becomes 0. The remainder so obtained are then read in the reverse order to obtain the octal equivalent of the decimal number.
For conversion of the fractional part of the decimal number, use the method of successive multiplication by 8. The carry so obtained is then read in the forward order to obtain the octal equivalent of the decimal number.
Example - 127.3510 = ( )10?
For Integer Part:
Quotient |
| Remainder |
127÷8=15 | Yielding a remainder of | 7 LSB |
15÷8=1 | Yielding a remainder of | 7 |
1÷8=0 | Yielding a remainder of | 1 MSB |
-------And so on-------- | ||
Octal equivalent number is 177.
For Fractional Part:
Product | Fraction |
| Carry |
0.35*8=2.80 | 0.80 | And a carry of | 2 |
0.80*8=6.40 | 0.40 | And a carry of | 6 |
0.40*8=3.20 | 0.20 | And a carry of | 3 |
-------And so on-------- | |||
The octal fraction is 0.26310.
If greater accuracy is desired, the process of successive multiplication can be continued further.
The octal equivalent is 177.2638.